Word of the Day: Concinnitas

The following quote was found here (The Mathematics of Palladio's Villas - Stephen R. Wassall)

"The very same numbers that cause sounds to have that concinnitas, pleasing to the ears, can also fill the eyes and mind with wondrous delight." - Leone Battista Alberti, De re aedificatoria (On the Art of Building in Ten Books)

which led me here.

"...the three principal components of that whole theory into which we inquire are number, what we might call outline, and position. But arising from the composition and connection of these three is a further quality in which beauty shines full face: our term for this is concinnitas" 


I have found myself struggling with the obsession of Geometric Analysis of local works by Jefferson. Perhaps more focus should be placed in the importance of the concinnitas of his work.

What Are The Mathematics of Jazz?

Clayton Cameron - What are the Mathematics of Jazz?

A-Rhythm-etic. The Math Behind the Beats
Part 3 of the TED Radio Hour episode Solve For X
http://www.npr.org/2015/03/06/388519359/what-are-the-mathematics-of-jazz

Mathematics of Music by Sir James Jeans

The following is the outline of a paper by Sir James Jeans found in The World of Mathematics, Volume 4, page 2278. This paper follows the same outline as his text, Science and Music, written in 1937. The text also includes chapters on Vibrations of Air, Harmony and Discord, and The Concert Room.

Mathematics of Music by Sir James Jeans

1. Tuning-Forks and Pure Tones
1. Pure Tone
2. Period, Frequency and Pitch
3. General Theory of Vibrations
4. Simultaneous Vibrations
5. Sound Curves of a Tuning Fork
6. Energy
7. Simultaneous Sounds
8. Superposing Vibrations of the Same Period
2. The Vibrations of Strings and Harmonics
1. Experiments with a Monochord
2. Mersenne’s Laws
3. Harmonic Analysis
4. String Plucked at its Middle Point
5. Analysis of a Sound-Curve
6. Natural Harmonics and Resonance
3. Hearing
1. The Threshold of Hearing
2. The Scale of Sound Intensity
3. The Threshold of Pain

http://www.amazon.com/Science-Music-Dover-Books/dp/0486619648 

Could the Babylonians have done this?

FACT: The Babylonians estimated the value of pi to be 3 1/8.
FACT: Based on the Plimpton Tablet, we know that the Babylonians were aware of "Pythagorian Triples".

UNCERTAINTY (for me personally): The Babylonians method of establishing the value of pi is based on the perimeter of a hexagon inscribed within a circle. I am still searching for specifics as to how this determines the value of the perimeter of the hexagon to be 25/8.

QUESTION: Could this approximation of squaring the circle have been used by the Babylonians?

The Three Geometric Problems of Greek Antiquity

The Delian Problem

To the complete the trifecta, below is my method on how to estimate the construction of doubling the volume of a given cube.

The Delian Problem [from wikipedia]: The problem owes its name to a story concerning the citizens of Delos, who consulted the oracle at Delphi in order to learn how to defeat a plague sent by Apollo. According to Plutarch it was the citizens of Delos who consulted the oracle at Delphi, seeking a solution for their internal political problems at the time, which had intensified relationships among the citizens. The oracle responded that they must double the size of the altar to Apollo, which was a regular cube. The answer seemed strange to the Delians and they consulted Plato, who was able to interpret the oracle as the mathematical problem of doubling the volume of a given cube, thus explaining the oracle as the advice of Apollo for the citizens of Delos to occupy themselves with the study of geometry and mathematics in order to calm down their passions.

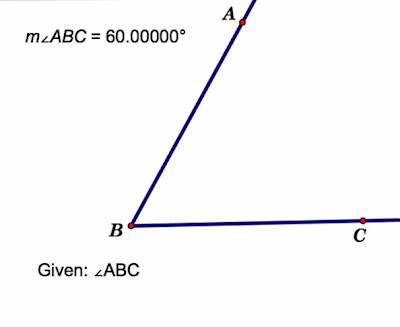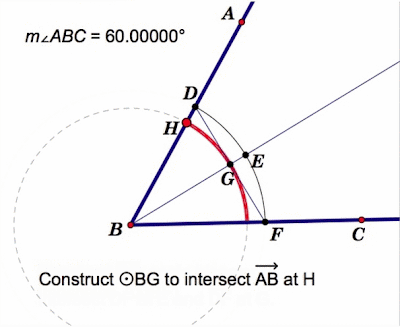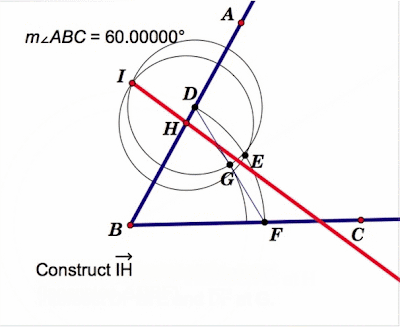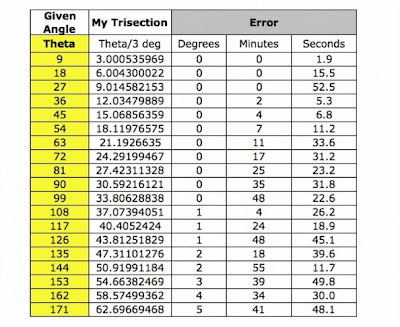
Trisecting an Angle

This is my recent attempt at approximating the trisection of an angle. See links below for sketchpad file and excel spreadsheet. The real point to be made here is that this is proven to be impossible. So, why bother trying? 

Sketchpad  - Excel Spreadsheet