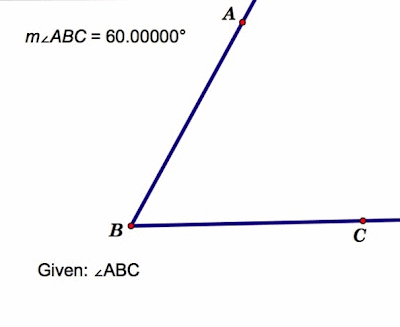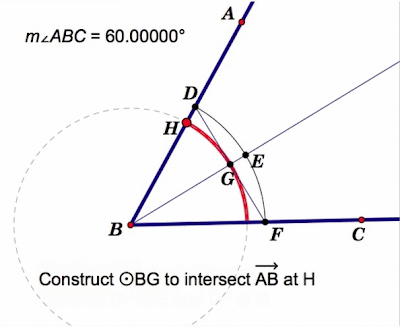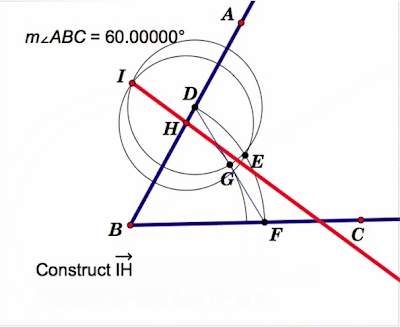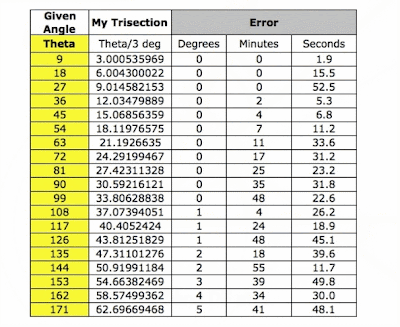
The following is the outline of a paper by Sir James Jeans found in The World of Mathematics, Volume 4, page 2278. This paper follows the same outline as his text, Science and Music, written in 1937. The text also includes chapters on Vibrations of Air, Harmony and Discord, and The Concert Room.
Mathematics of Music by Sir James Jeans
- Tuning-Forks and Pure Tones
- Pure Tone
- Period, Frequency and Pitch
- General Theory of Vibrations
- Simultaneous Vibrations
- Sound Curves of a Tuning Fork
- Energy
- Simultaneous Sounds
- Superposing Vibrations of the Same Period
- The Vibrations of Strings and Harmonics
- Experiments with a Monochord
- Mersenne’s Laws
- Harmonic Analysis
- String Plucked at its Middle Point
- Analysis of a Sound-Curve
- Natural Harmonics and Resonance
- Hearing
- The Threshold of Hearing
- The Scale of Sound Intensity
- The Threshold of Pain
http://www.amazon.com/Science-Music-Dover-Books/dp/0486619648